Validación de las ecuaciones predictivas del consumo de oxígeno y nuevas fórmulas para el entrenamiento interválico

Bruno Bazuelo-Ruiz

Helios de Rosario

Juan V. Durá-Gil

Resumen

Objetivos. Nuestro objetivo era determinar si existe alguna diferencia significativa entre el gasto energético calculado y previsto en las ecuaciones predictivas de uso más frecuente en la literatura, así como desarrollar una nueva ecuación predictiva específica para el entrenamiento interválico aeróbico con una muestra más transversal de la población en términos de edad, forma física e índice de masa corporal (IMC).
Métodos. Se reclutó a veinte participantes sanos para el estudio. Se establecieron dos grupos de personas, en función de su IMC. El grupo con un IMC bajo tenía un IMC de entre 19 y 22 y el grupo con un IMC alto, uno de entre 26 y 29. El protocolo de las pruebas consistía en realizar 12 rutinas de intensidades individualizadas, 6 velocidades andando y 6 corriendo en cinta, y medir tanto la frecuencia cardíaca como el gasto energético. El tiempo de reposo entre intervalos varió de 1 a 2 minutos.
Resultados principales. Se detectó que el consumo de oxígeno medido era significativamente distinto del predicho por las ecuaciones relativas tanto al ejercicio de andar como de correr seleccionadas entre la literatura. De entre las comprobadas, la ecuación de Léger fue la que arrojó mejores resultados para calcular el consumo de oxígeno al andar y la fórmula ACSM demostró ser la mejor para correr. Sin embargo, se comprobó que ninguna de las dos ofrecía una alta precisión.
Conclusiones. Las ecuaciones predictivas seleccionadas de la literatura para este estudio no demostraron ser lo bastante precisas para calcular el consumo de oxígeno durante el entrenamiento interválico aeróbico. En este trabajo se proponen cuatro fórmulas nuevas para mejorar el cálculo del gasto metabólico en actividades interválicas en una población con características más amplias que las encontradas en la literatura.

Introducción 

El estudio del cálculo del gasto metabólico durante el ejercicio físico se practica desde hace mucho tiempo debido a su relevancia para la prescripción de rutinas de ejercicio personalizadas. Contar con un conocimiento más preciso del gasto energético (GE) resulta útil tanto a la comunidad médica como a los entrenadores deportivos y a los pacientes. Caminar y correr son las dos actividades físicas más recomendadas en poblaciones que desean mejorar su calidad de vida. De hecho, la mayoría de ecuaciones de predicción del GE se centran en las modalidades de caminar y correr. Dentro de estas modalidades, sigue desconociéndose qué factores clave –como el volumen, la frecuencia, la intensidad y la densidad– son los más determinantes en cada caso. Por tradición, médicos y entrenadores deportivos recomiendan practicar ejercicio de intensidad moderada constante (EIMC). Sin embargo, nuevas modalidades de ejercicio, como el entrenamiento interválico aeróbico (EIA), han cobrado popularidad debido a que consiguen una mayor adherencia a la práctica y (Currie et al., 2013) mayores beneficios en comparación con el EIMC (Hwang et al., 2011; Warburton et al., 2005). Los ejercicios interválicos pueden definirse como breves fases de ejercicio intenso seguidas por breves pausas de recuperación. Los principales beneficios detallados en estudios previos incluyen mejoras en la función endotelial y mitocondrial (Wisløff et al., 2007), una mejora de la capacidad funcional (Daussin et al., 2007; Helgerud et al., 2007) y la prevención de enfermedades cardiovasculares (Kemi & Wisloff, 2010). Todas estas mejoras pueden comportar mejor calidad de vida (Nilsson et al., 2008). Además, muchas personas pueden beneficiarse de este tipo de ejercicio, tanto si están sanas (Tsukamoto et al., 2016) como si son pacientes con cardiopatías (Rognmo et al., 2004). 

La determinación directa del GE es cara y lenta y está sujeta a las condiciones de los laboratorios. Por otro lado, una alternativa válida es el cálculo del consumo de oxígeno realizado con las ecuaciones predictivas presentes en la literatura. La mayoría de las variables medidas para este cálculo fueron parámetros de aceleración (Bouten et al., 1994; Staudenmayer et al., 2009), señales de frecuencia cardíaca (FC) (Keytel et al., 2005; Pettitt et al., 2007) o parámetros espaciotemporales (Glass et al., 2007; Hall et al., 2004; Loftin et al., 2010). Ahora bien, un punto débil de estas ecuaciones es que la población utilizada en la mayoría de las investigaciones era muy similar, por lo general, estaba integrada por participantes jóvenes y sanos. Además, todas las ecuaciones se diseñaron para la práctica de ejercicio submáximo ininterrumpido.

De ahí que los objetivos del trabajo fueran (i) determinar si existe alguna diferencia significativa entre el gasto energético (GE) calculado y previsto en las ecuaciones predictivas de uso más frecuente en la literatura, y (ii) desarrollar una nueva ecuación de predicción específica para el entrenamiento a intervalos aeróbico con una muestra más transversal de la población en términos de edad, forma física e índice de masa corporal (IMC).

Metodología

Participantes 

Se reclutó a veinte participantes sanos (10 hombres y 10 mujeres) para esta investigación. Se establecieron dos grupos de personas en función de su índice de masa corporal (IMC). Las características de los participantes en el estudio fueron las siguientes: IMC bajo (5 hombres y 5 mujeres): edad 30±9.2 años; masa corporal 59.17 ± 8.71 kg; peso 1.71 ± .13 m; IMC 20.17 ± .81; IMC alto (5 hombres y 5 mujeres): edad 40.2 ± 9.3 años; masa corporal 78.86 ± 13.63 kg; altura 1.67 ± .14 m; IMC 28.17 ± 1.17. El grupo con un IMC bajo se situaba entre un 19 y un 22 y el grupo con un IMC alto, entre 26 y 29. Todos los participantes declararon no sufrir cardiopatías ni lesiones que pudieran limitar su capacidad para someterse al ensayo. Los participantes se comprometieron a no practicar ejercicio extenuante durante las 24 horas previas y a no consumir cafeína al menos durante las 6 horas previas a cada sesión de comprobación. El protocolo del estudio se adhería a los principios de la Declaración de Helsinki y recibió la aprobación del Comité Ético de la Universidad Politécnica de Valencia. Todos los participantes dieron su consentimiento informado por escrito.

Procedimiento

El protocolo del ensayo consistía en practicar 12 intensidades personalizadas, 6 velocidades caminando y 6 corriendo. Dichas velocidades se establecieron a medida que los participantes calentaban, con acuerdo al nivel de forma física de cada uno de ellos. Tanto para las modalidades de caminar como de correr los participantes debían informar de tres velocidades. Para la modalidad de caminar, la primera era una velocidad cómoda a la que los participantes estaban acostumbrados a caminar normalmente; la segunda era una velocidad a la que podían caminar y correr despacio. Este espectro se subdividió en 6 partes para obtener las 6 velocidades de marcha. La velocidad de marcha máxima sirvió como velocidad de correr mínima (jogging ligero). La velocidad de correr máxima se estableció con acuerdo a la velocidad que los participantes fueron capaces de mantener durante al menos 4 minutos sin mostrar signos visibles de un elevado nivel de fatiga. Asimismo, el espectro entre las velocidades de correr mínima y máxima se subdividió para obtener las 6 velocidades de correr. Una vez establecidas sus velocidades individuales, todos los participantes practicaron las 12 velocidades distintas en un orden aleatorio. El motivo para establecer este número de repeticiones o velocidades era analizar si las ecuaciones predictivas funcionaban correctamente en las distintas intensidades de caminar y correr o solo en una. Los ejercicios a cada velocidad tuvieron una duración de 3 minutos con una pausa de descanso de 1 minuto entre ejercicios de caminar y 2 minutos entre ejercicios de correr. Tres minutos ofrecían un tiempo suficiente para medir un consumo de oxígeno estable (Nieman, 2010). A partir de este tiempo, los últimos dos minutos de cada velocidad se utilizaron para analizar el gasto energético (Nieman, 2010). Antes del calentamiento, la frecuencia cardíaca en reposo (FC_reposo) y el gasto energético se calcularon durante un lapso de 5 minutos en posición sentada.

Material e instrumentos

Las pruebas se realizaron en una cinta de caminar calibrada (HP Cosmos, Mercury, Alemania) con un grado del 1% (Jones y Doust, 1996). Las señales de la FC se midieron con un aparato nECG MINDER (Nuubo, España) colocado en el pecho de los participantes. El gasto energético se calculó mediante calorimetría indirecta, usando la espirometría de circuito abierto del analizador metabólico Cosmed K4b2 (Roma, Italia). El analizador de gas se calibró cada mañana antes del inicio de las pruebas. 

Análisis de datos 

La literatura recoge el uso de múltiples fórmulas para calcular el consumo de oxígeno. Seleccionamos las siguientes ecuaciones predictivas porque son las que tanto los fisiólogos como los investigadores utilizan más frecuentemente en sus estudios.

Caminar:

EQ1 (Glass et al., 2007): VO₂ (ml/kg/min) = .1 * S  1.8 * S *grado fraccionario + 3.5; donde S es la velocidad en m/ min y el grado fraccionario se presenta en forma decimal, el grado de 5 % es .05.

EQ2 (Van der Walt & Wyndham, 1973): VO₂ (L/min): .00599 * M + .000366 * M * V²; donde M es masa corporal (kg) y V: velocidad (m/s).

EQ3 (Léger & Mercier, 1984): VO₂ (ml/kg/min) = 2.209 + 3.1633 * V; donde V es la velocidad caminando en km/h.

EQ4 (Pettitt et al., 2007): METS = 6 * FC_índice - 5;
FC_índice = FC_absoluta / FC_reposo

EQ5 (Keytel et al., 2005): EE (kJ/min) = sexo * (-55.0969 + .6309 * frecuencia cardíaca + .1988 * peso + .2017 * edad) + (1 - sexo) * (-20.4022 + .4472 * frecuencia cardíaca – .1263 * peso + .074 * edad); donde Hombre = 1, Mujer = 0; 1 l O₂/min = 20 kJ/min.

Correr:

EQ6 (Glass et al., 2007): VO₂ (ml/kg/min) = .2 * S + .9 * S * grado fraccionario + 3.5; donde S es la velocidad en m/min y el grado fraccionario se presenta en forma decimal, el grado de 5 % es .05.

EQ7 (Van der Walt & Wyndham, 1973): VO₂ (L/min): - .419 + .03257 * M + .000117 * M * V²; donde M es masa corporal (kg) y V: velocidad (m/s).

EQ8 (Léger & Mercier, 1984): VO₂ (ml/kg/min) = 2.209 + 3.1633 * V; donde V es la velocidad corriendo en km/h.

EQ9 (Pettitt et al., 2007): METS = 6 * FC_índice - 5; FC_índice= FC_absoluta / FC_reposo; 1MET = 3.5 ml/kg/min.

EQ10 (Keytel et al., 2005): EE (kJ/min) = sexo * (-55.0969 + .6309 * frecuencia cardíaca + .1988 * peso + .2017 * edad) + (1 - sexo) * (-20.4022 + .4472 * frecuencia cardíaca - .1263 * peso + .074 * edad); donde Hombre = 1, Mujer = 0; 1 l O₂/min = 20 kJ/min.

Antes de acometer el análisis estadístico, los resultados obtenidos con cada ecuación se convirtieron a ml/kg/min con el fin de unificarlos y poder compararlos. Se realizó una prueba T de comparación para calcular la diferencia y la significancia de los valores VO₂ calculados y estimados de cada ecuación utilizada. Para calcular la magnitud del error también se tuvieron en cuenta los valores absolutos de las diferencias entre los valores calculados y los medidos. La significancia estadística se fijó en un nivel del .05. A partir de ahí se generaron distintos niveles de correr y caminar mediante un análisis de regresión lineal múltiple con vistas a mejorar la precisión en esta población y este tipo de actividad física (entrenamiento interválico). Los modelos se ajustaron en función de la FC_índice, el IMC, el sexo, la velocidad y la edad. La FC_índice es la media absoluta de la FC dividida por la FC_reposo.

Resultados 

El intervalo de velocidades (media ± DT) para la modalidad de caminar fue de entre .71 ± .12 m·s-¹ y 1.74 ± .31 m·s-¹ y de 1.74 ± .31 m·s-¹ a 2.55 ± .67 m·s-¹ en la modalidad de correr.

Se detectó que el VO₂ calculado difería significativamente (p < .05) de todas las fórmulas predictivas para caminar y correr utilizadas en este análisis. En el caso de la actividad de caminar, la Tabla 1 mostró que EQ1, EQ2 y EQ4 subestiman el VO₂ medido y EQ3 y EQ5 lo sobreestiman. En el caso de la actividad de correr, EQ6, EQ7, EQ8 y EQ9 subestiman el VO₂ medido y EQ10 lo sobreestima.

Se analizan las variables independientes que afectan a los modelos de caminar y correr y proponemos dos modelos para cada caso, en función de si se utiliza o no la señal de la FC como variable independiente. El primer modelo obtenido se utilizó con todas las variables (FC_índice, IMC, sexo, velocidad y edad), pero el IMC (alto y bajo) y el sexo (hombre o mujer) no demostraron ser significativos (p > .05), motivo por el cual dichas variables se excluyeron de los modelos finales. La Tabla 2 muestra los coeficientes de los modelos para la modalidad de caminar utilizando la FC_índice como variable independiente, mientras que la Tabla 3 muestra el modelo para la modalidad de caminar sin la FC_índice. Las tablas 4 y 5 muestran los coeficientes de los modelos para la modalidad de correr con y sin la FC_índice, respectivamente.

Tabla 1
Valores VO₂ calculados y estimados y diferencia entre el cálculo y la estimación andando (EQ1-EQ5) y corriendo (EQ6-EQ10). Valores expresados en ml·kg·min-1 (media ± DT).

Ver tabla

Tabla 2
Coeficientes y significancia para el modelo de regresión lineal múltiple ajustado por edad, FC_índicey velocidad al caminar.

Ver tabla

Tabla 3
Coeficientes y significancia para el modelo de regresión lineal múltiple ajustado por edad y velocidad al caminar.

Ver tabla

Tabla 4
Coeficientes y significancia para el modelo de regresión lineal múltiple ajustado por edad, FC_índice y velocidad al correr.

Ver tabla

Tabla 5
Coeficientes y significancia para el modelo de regresión lineal múltiple ajustado por edad y velocidad al correr.

Ver tabla

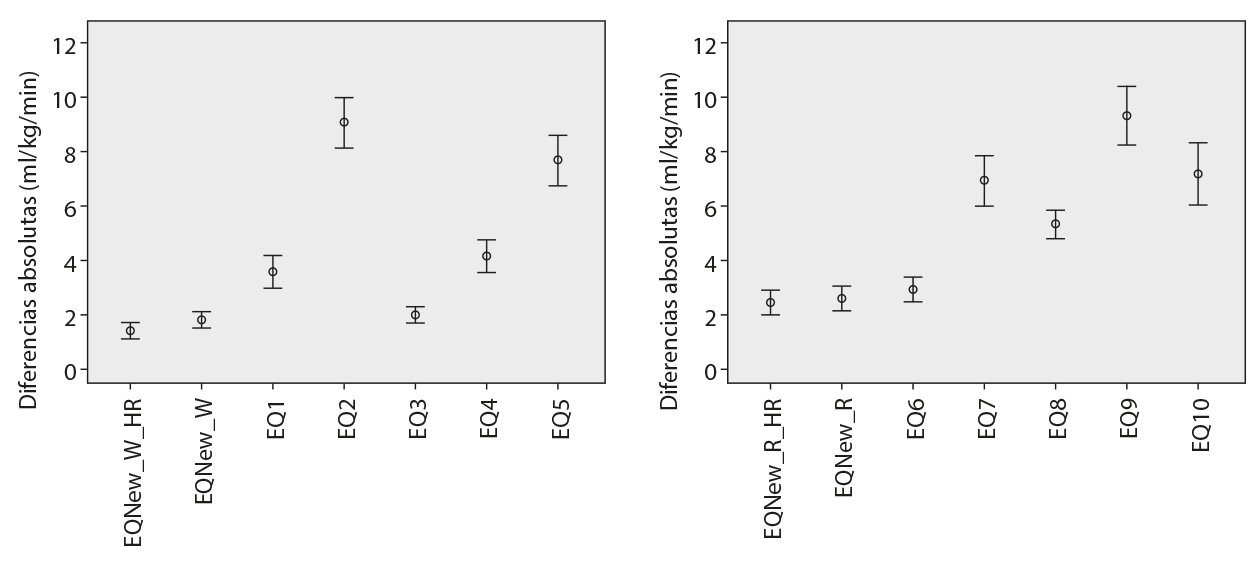
Los modelos de regresión generados ofrecen una ecuación predictiva más precisa tanto para la actividad física de caminar como de correr en esta población. La Figura I muestra que nuestras ecuaciones predictivas presentan un error absoluto inferior (media ± DT) con respecto al VO₂ calculado. Las diferencias absolutas de nuestras ecuaciones predictivas para la actividad física de correr fueron de 2.60 ± 2.47 ml·kg·min-¹ y 2.79 ± 2.40 ml·kg·min-¹, cuando se incluyeron y excluyeron las señales de FC, respectivamente. En el caso de la actividad física de caminar, mejoramos en mayor grado aún la estimación de VO₂ con las diferencias absolutas de 1.44 ± 1.17 l·kg·min-¹ y 1.79 ± 1.52 ml·kg·min-¹ cuando las señales de FC se incluyen y excluyen, respectivamente.

Discusión

Este estudio se concentraba en medir el consumo de oxígeno durante el entrenamiento interválico aeróbico en una población con demandas energéticas y valores de IMC distintos. En primer lugar, se comparó la precisión del consumo de O₂ medido y estimado para el EIA. A continuación, al detectar que no era lo bastante precisa, se propusieron cuatro fórmulas nuevas para mejorar el cálculo del gasto metabólico en actividades interválicas en una población con características más variadas que las encontradas en la literatura previa.

La muestra utilizada en la mayoría de los estudios son personas jóvenes, sanas y con un peso normal, con un IMC inferior a 25 (Glass et al., 2007). La muestra consistió en participantes con distintas características no comprobadas previamente. La muestra de Hall et al. (2004) era diferente. En este caso se reclutó a un total de 24 participantes con un IMC que iba de 20 a 27.4; sin embargo, la media del IMC de las mujeres y los hombres era de 22.37 y 23.64, respectivamente. Otra diferencia entre ambos estudios es la media de edad, que en el suyo se sitúa en 21.4 años en el caso de las mujeres y 23.2 en el caso de los hombres. Por su parte, Loftin et al. (2010) desarrollaron una ecuación predictiva para una población similar a la de nuestro estudio, pero el cálculo de GE era para una distancia determinada (1.6 km) en lugar de durante un tiempo o a una velocidad concretos, que son las variables que suelen utilizarse en el entrenamiento interválico. 

Figura 1

Ver a tamaño completo

La especificidad de la actividad empleada para medir el consumo de oxígeno en la actividad de entrenamiento es relevante si se busca precisión. Fisiólogos y entrenadores suelen utilizar las ecuaciones de ACSM (Glass et al., 2007) con frecuencia en la literatura, pese a que presentan ciertas limitaciones. Se diseñaron para rutinas de ejercicio constantes y dependen de un intervalo de velocidad concreto (de .83 a 1.66 m·s-¹ en la ecuación para la actividad física de caminar y superior a 2.22 m·s-¹ en la ecuación correspondiente a la actividad física de correr). Por consiguiente, queda por cubrir un hueco en el intervalo de velocidades que va de 1.66 a 2.22 m·s-¹. Además, en algunos estudios, como (Hall et al., 2004; Koutlianos et al., 2013; Loftin et al., 2010; Peterson et al., 2003), se usaron ecuaciones predictivas de ACSM con validación cruzada y se concluyó que no sirven para predecir con precisión el consumo de O₂. Ello se debe a la aplicación de estas fórmulas a distintos protocolos o modalidades de ejercicio. 

Weyand et al. (2013) averiguaron que la ecuación predictiva de ACSM para la actividad física de caminar subestimaba de forma significativa la tasa metabólica. Nuestros resultados coincidían con este estudio, pero indicaban que la EQ3 era la mejor de las ecuaciones comprobadas para calcular el consumo de O₂ en la modalidad de caminar y que EQ6 era la que ofrecía mejores resultados para la modalidad de correr. Sin embargo, ninguna de ellas es lo bastante precisa (p < .05) cuando se compara con los valores medidos. En el caso de la actividad física de correr, las peores ecuaciones predictivas demostraron ser las que utilizan señales de FC como entrada para calcular el gasto metabólico.

El GE al caminar y correr es distinto, más elevado en la segunda actividad. Nuestra investigación también determinó que el GE en la modalidad de correr era más elevado que en la de caminar para la misma velocidad absoluta. Por consiguiente, tal como se indica en otras investigaciones (Glass et al., 2007; Van der Walt y Wyndham, 1973), era preciso diseñar ecuaciones distintas para las actividades de caminar y correr.

Hasta lo que se ha estudiado, no existen ecuaciones capaces de predecir con precisión el consumo de O₂ en el EIA en una población con distintos valores de IMC. De ahí que se hayan desarrollado dos ecuaciones predictivas, una para caminar y otra para correr, que incluyen las variables de la edad (años), la velocidad (en km/h) y la FC_índice (FC_absoluta / FC_reposo):

Caminar:

EQNew_W_HR (ml/kg/min) = 13.031 – .068 * Edad + .586 * Velocidad² + 2.088 * FC_índice – 2.454 * Velocidad

EQNew_W (ml/kg/min) = 15.227 – .055 * Edad + .603 * Velocidad² - 2.425 * Velocidad

Correr:

EQNew_R_HR (ml/kg/min) = 6.415 – .087 * Edad + 3.051 * FC_índice+ 2.877 * Velocidad

EQNew_R (ml/kg/min) = 9.302 – .047 * Edad + 3.107 * Velocidad

Se descubrió que incluir la FC_índice para calcular el consumo de VO₂ posibilitaba una mayor precisión. No obstante, en el caso de una intensidad de ejercicio dada, a medida que la temperatura ambiente aumenta, la FC también aumenta sin que se produzca por ello un incremento correspondiente en el GE (Hebestreit y Bar-Or, 1998). 

Conclusión

Las ecuaciones predictivas seleccionadas de la literatura para este estudio no demostraron ser lo bastante precisas para calcular el consumo de oxígeno durante el entrenamiento interválico aeróbico. Proponemos cuatro fórmulas nuevas para mejorar el cálculo del gasto metabólico en actividades interválicas en una población con características más amplias que las encontradas en la literatura. Desde una perspectiva práctica, en condiciones reales las ecuaciones deben emplearse con precaución. Además, las ecuaciones propuestas pueden utilizarse para calcular el consumo de oxígeno en actividades interválicas aeróbicas, como caminar o correr, si bien advertimos que dichas fórmulas no se han sometido a validación cruzada. Convendría que las validaran nuevos estudios.